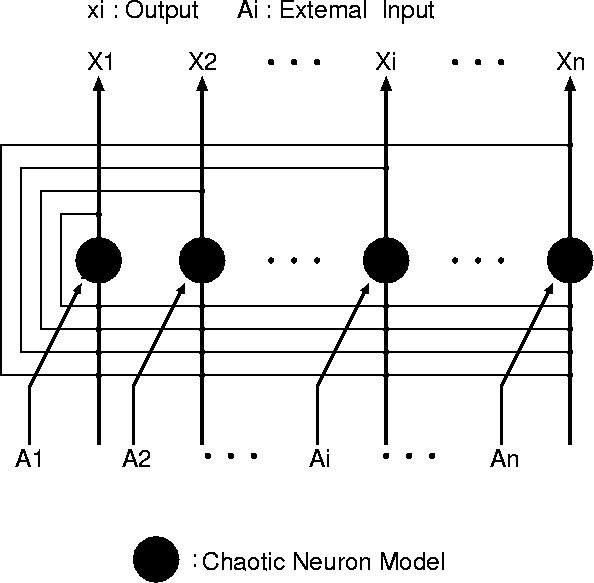
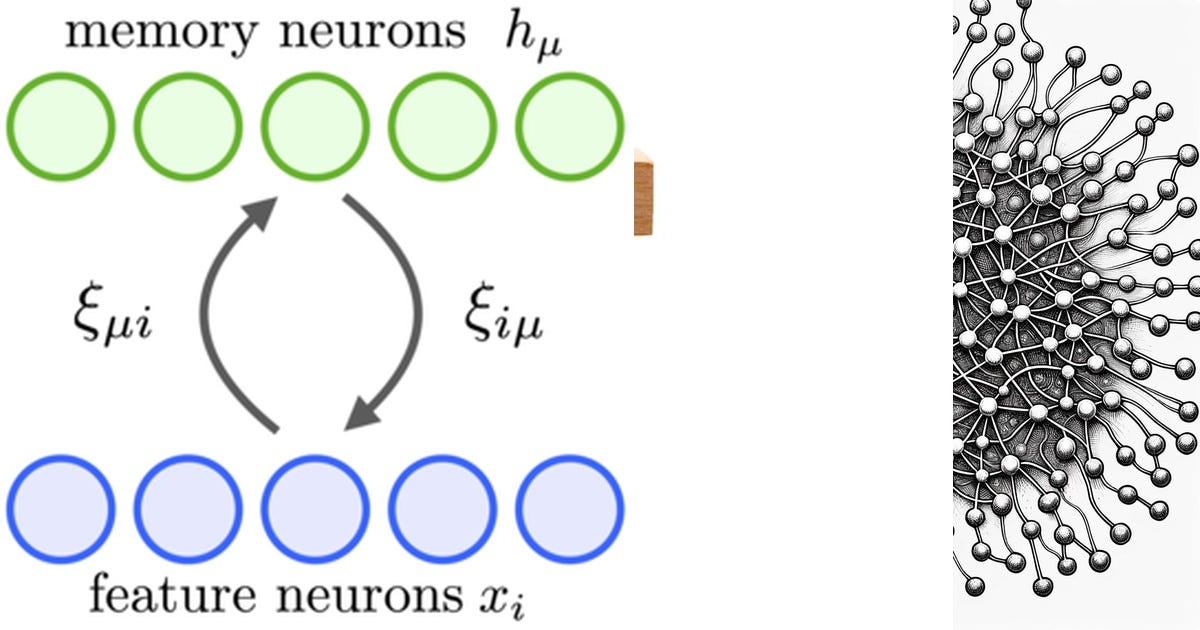
ホップフィールド・ネットワーク

ホップフィールド・ネットワーク (英: Hopfield network) は、ニューラルネットワークの一モデルである。

アメリカ合衆国の物理学者であるジョン・ホップフィールド (J.J. Hopfield) が提唱した。ユニット（ニューロン）間に対称的な相互作用がある非同期型ネットワークであり、自然な操作によってネットワークのエネルギーが極小値をとる。元はスピンの安定条件をもとめるモデルとして発想されたものであったが、ネットワークによる連想記憶のモデルとして歓迎され、ニューラルネットブームの火付け役の一つとなり、また後のボルツマンマシンの元ともなったが、ボルツマンマシンでは統計的なゆらぎをもちいることで系のエネルギーの極小値ではなくて最小値をとることを目指すモデルであることが異なる。

構造と動作

各ユニットはMcCulloch-Pitts 型入出力特性をもっている。

タイムスライス${\displaystyle t}$において、${\displaystyle w_{ij}(t)}$をユニットjからiへの結合係数、${\displaystyle -\theta _{i}(t)}$をユニットiの閾値、${\displaystyle x_{i}(t)}$をユニットiの出力とする。ここで全てのi, jの組について、i ≠ jならば${\displaystyle w_{ij}(t)=w_{ji}(t)}$、i = jならば${\displaystyle w_{ij}(t)=0}$である。またネットワーク全体のエネルギー${\displaystyle E(t)}$を、次のように定義する

${\displaystyle E(t)=-{1 \over 2}{\sum _{i\neq j}{w_{ij}{x_{i}(t)}{x_{j}(t)}}}-\sum _{i}{\theta _{i}(t)}{x_{i}(t)}}$

以上の構造を持つモデルをタイムスライス毎に次のように動作させる

1. ランダムにユニットを一つ選ぶ
2. そのユニットへの入力の重み付き総和を計算する
3. 結果に基づき、そのユニットの出力を更新する
   • 閾値より大きければ1
   • 閾値と等しければ現在と同じ値
   • 閾値より小さければ0
   • （この際、他のユニットには手を触れない）
4. tを増分だけ増加させ最初に戻る

すると、${\displaystyle E(t)}$はtの増加と共に単調減少することが容易に示される。

参考文献

• 西森秀稔：「スピングラスと連想記憶」、岩波書店、ISBN4-00-011156-6 (2003年1月29日). 第3章.

外部リンク

• Hopfield Network - ウェイバックマシン（2007年1月6日アーカイブ分） - スカラーペディア百科事典「ホップフィールド・ネットワーク」の項目。